Página editada por Antonio L. Manzanero, profesor de la Facultad de Psicología de la Universidad Complutense de Madrid. España

Psicofísica sensorial

Definición:
  • Fechner (1860): Teoría exacta de la relación entre cuerpo y mente.
  • Jáñez (1992): El estudio de la relación entre la magnitud física de los estímulos y la intensidad de las sensaciones subjetivas que suscitan. 
Objetivo:
  • Determinar la relación entre la magnitud física (E) y la intensidad subjetiva (S)

Teoría del umbral sensorial

lNecesidad de un nivel mínimo en la intensidad de la estimulación, por debajo del cual no suscita sensación subjetiva alguna. 
Definición de Umbral: 
  • Fechner (1860): punto en que un estímulo o una diferencia entre estímulos comienza a ser perceptible o desaparece. 
    • Imposibilidad de encontrar un valor exacto de estimulación.
  • Guilford (1954): la pequeña cantidad de estímulo que es percibido un 50 % de las veces. (definición operativa) 


Umbral absoluto y sensibilidad

Umbral Absoluto (Eo): mínima intensidad que tiene que tener un estímulo para ser percibido. 
  • A esta magnitud en el continuo físico, le corresponde el valor "0" en la escala psicológica o escala de sensación.
Sensibilidad (SS): capacidad para percibir el estímulo. 
  • Es el recíproco del umbral
SS = 1 / Eo
  • A un umbral alto corresponde un sensación baja 


Umbral diferencial
  • Umbral Diferencial (ΔE): mínima diferencia perceptible.
    • incremento mínimo en la magnitud del estímulo requerido para que el sujeto sea consciente de que ha habido un cambio. 
  • Diferencia apenas perceptible (ΔS): la unidad de medida en la escala de sensación. 


Métodos psicofísicos para determinar umbrales sensoriales 
  • Método de los estímulos constantes.
  • Método de los límites.
  • Método de ajuste.
Método de los estímulos constantes
lLas intensidades de los estímulos utilizados están establecidas previamente y no se modifican durante el experimento.
  • Proceso:
    • Determinación del umbral absoluto Eo 
    • Determinación del umbral diferencial ΔE 
lDeterminación del umbral absoluto (Eo)
  • Selección de las intensidades de los estímulos
    • Dos intensidades extremas: a) una casi siempre percibida y b) una casi siempre imperceptible
    • Establecimiento de estímulos intermedios (min. 7)
  • Prueba experimental
    • Presentación aleatoria de los estímulos (n = 100)
    • Cálculo de la proporción (%) de veces que se ha percibido cada estímulo
  • Cálculo de Eo
    • Estímulo percibido un 50% de las veces (3 métodos)
      • Percentil 50
      • Interpolación lineal
      • Mínimos cuadrados 
lPercentil 50
 
      E     f      P
10 1 0,05
15 2 0,1
20 4 0,2
25 6 0,3
30 10 0,5
35 14 0,7
40 17 0,85
45 18 0,9
50 19 0,95

n=20

Interpolación lineal
E f P
6 2 0,10
8 4 0,20
10 5 0,25
12 8 0,40
14 13 0,65
16 17 0,85
18 18 0,90
20 19 0,95

n=20
Mínimos Cuadrados:
Trasformación de las puntuaciones directas en típicas y cálculo de la recta de regresión de z sobre E
z’ = aE + b
0 = aEo + b

Z1 = puntuación típica que en una distribución normal deja por debajo un área igual a la proporción de veces que fue percibido el estímulo E1.

XY

EfPZ

620,10-1,28

840,20-0,84b=0,22
1050,25-0,67a=-2,69
1280,40-0,25

14130,650,39
Z' = -2.69 + 0.22E
16170,851,04
0 = -2.69 + 0.22 E
18180,901,28
Eo = 12.27
20190,951,64



rez=0,99
n=20

l  
Determinación del umbral diferencial (ΔE)  
  • Selección de los estímulos
    • Un único estímulo estándar
    • Conjunto de estímulos de comparación (aprox. 9): a) el más intenso casi siempre percibido como mayor que estándar, y b) el menos intenso casi siempre percibido como menor que estándar.
  • Prueba experimental
    • Presentación aleatoria del estímulo estándar acompañado de estímulo de comparación. Decisión cuál mayor.
    • Cálculo de la proporción (%) de veces que se ha percibido cada estímulo como mayor que el estándar.
  • Cálculo de ΔE
    • Normalización de las puntuaciones.
    • Cálculo del punto de igualdad subjetiva. Ei juzgado mayor que el estándar el 50 % de las veces.
    • Cálculo de ΔE superior e inferior (75 y 25 % de las veces). 



















Método de los límites

  • Se alternan series de estímulos de intensidad ascendente con series de intensidad descendente
  • Cálculo del umbral 
    • Para serie ascendente: el límite es el primer estímulo perceptible. (menos a más) 
    • Para la serie descendente: el límite es el primer estímulo imperceptible. (más a menos)
Determinación del umbral absoluto (Eo)
  • Selección de estímulos:
    • Dos intensidades extremas: a) una casi siempre percibida y b) una casi siempre imperceptible
    • Establecimiento de estímulos intermedios (min. 7)
  • Prueba experimental:
    • Se presentan alternativamente series crecientes y decrecientes, hasta el punto de perceptibilidad / imperceptibilidad.
  • Cálculo de Eo
    • Punto de transición: media de los dos últimos E presentados
    • Umbral absoluto: media de los puntos de transición
l
E A D A D A D A D A D
10
SI SI SI SI SI
9
SI
SI
SI
SI
SI
8
SI
SI
SI
SI
SI
7
SI
SI
SI SI SI
SI
6
SI SI NO
SI NO SI SI SI
5 SI NO NO
SI SI NO NO NO SI
4 NO
NO
NO NO NO
NO NO
3 NO
NO
NO
NO
NO
2 NO
NO
NO
NO
NO
1 NO
NO
NO
NO
NO
4,5 5,5 5,5 6,5 4,5 4,5 6,5 5,5 5,5 4,5

 
Eo= (4,5 + 5,5 + 5,5 + 6,5 + 4,5 + 4,5 + 6,5 + 5,5 + 5,5 + 4,5)/10 = 5,3
l
l


Determinación del umbral diferencial (ΔE):
  • Estímulos:
    • Un único estímulo estándar
    • Conjunto de estímulos de comparación (aprox. 9): a) el más intenso casi siempre percibido como mayor que estándar, y b) el menos intenso casi siempre percibido como menor que estándar.
  • Prueba experimental
    • Se presenta el E de prueba acompañado del E de comparación. Decisión mayor/igual/menor
    • Los ensayos se agrupan en series ascendentes y descendentes alternativamente
      • Serie ascendente comienza con estímulos de intensidad menor a al estándar, termina con el E de sensación mayor
      • Serie descendente comienza con estímulos de intensidad mayor al estándar. Termina con el E de sensación menor.


Método del ajuste

  • lEl propio sujeto controla la intensidad del estímulo.
  • Cálculo del umbral
    • Número de estímulos indeterminado 
lDeterminación del umbral absoluto (Eo) 
  • Selección de estímulos: 
    • Estímulos indeterminado. Dependen de cada sujeto. 
  • Prueba experimental: 
    • El sujeto calibra el punto donde un estímulo deja de ser percibido o empieza a serlo. 
  • Cálculo de Eo 
    • Media de los puntos definidos por el sujeto
l  
l
l

l
Determinación del umbral diferencial (ΔE):
  • Estímulos:
    • Un único estímulo estándar
    • Conjunto de estímulos de comparación.
  • Prueba experimental
    • Se presenta el E de prueba acompañado del E de comparación. Decisión: igualdad
  • Cálculo de ΔE:
    • Normalización de las puntuaciones (z).
    • Cálculo del punto de igualdad subjetiva. Ei juzgado igual que el estándar el 50 % de las veces.



Ley de Weber
ENUNCIADO: el umbral diferencial es proporcional a la intensidad que en ese instante posea el estímulo.
EXPRESIÓN FORMAL:

ΔE = K · E

Para que se cumpla la Ley, K debe de ser constante.

K = ΔE / E
K = constante de Weber
ΔE = incremento mínimo en la magnitud del estímulo necesario para percibir un cambio en la sensación
E = magnitud del estímulo
Crítica 
lNo para todos los estímulos y todas las intensidades el umbral diferencial crece proporcionalmente.

Modificaciones a la Ley de Weber
  • Ley de Weber Generalizada: El umbral diferencial (ΔE) es proporcional a la cuantía en que la intensidad del estímulo rebasa el umbral absoluto (Eo).
ΔE = K (E - Eo)
  • Ley raíz cuadrada de Fullerton y Cattell
ΔE = K √E
  • Ley potencial de Guilford:
ΔE = K · Es
Ley de Fechner
  • Asume la ley de Weber: 
ΔE = K · E
  • Asume la igualdad de las diferencias apenas perceptibles (ΔS):
ΔS = Q
  • “Principio matemático auxiliar”: las relaciones válidas para magnitudes finitas pequeñas son válidas para magnitudes infinitesimales.
ENUNCIADO: La magnitud de la Sensación es proporcional al Ln del número de veces que el estímulo rebasa el EO. 
EXPRESIÓN FORMAL:

S = k × Ln (E)

Ley Logarítmica: Si se incrementa la estimulación en proporción geométrica las sensaciones lo harán en progresión aritmética.
Críticas:
  • lInvalidez del supuesto de la ley de Weber
    • No se cumple para S muy bajas o muy altas
    • El tamaño de Eo depende del ruido => K variable
  • Las diferencias apenas perceptibles (ΔS) no son constantes con funciones no lineales.
  • Explica la relación de sonoridad y brillo pero no algunas otras como la sensación dolorosa.
  • Se produce un ajuste intermodalidades

La Ley de Stevens

EXPRESIÓN FORMAL:
lS  = K • Eb

ENUNCIADO: La Sensación es función potencial de la magnitud del Estímulo.

Diferencia Apenas Perceptible
Fechner: ΔS constante, con independencia del nivel de sensación. 
ΔS = q 
Brentano-Ekman: ΔS directamente proporcional al nivel de sensación (ley de Ekman).
ΔS = p × y


l 
Métodos de elaboración de escalas
Stevens: las relaciones existentes entre las magnitudes son un reflejo de las relaciones empíricas observadas entre los E.
  • La dureza de cada piedra depende de la mayor o menor dureza de otras piedras
Métodos:
  • Emparejamiento de Magnitudes
  • Emparejamiento de Razones
  • Emparejamiento de Intervalos
 
lEmparejamiento de magnitudes
  • Estimación de magnitudes:
    • El sujeto debe indicar la magnitud de estímulos con diferente intensidad presentados varias veces en orden aleatorio.
    • Las magnitudes asignadas a los E deben guardar la misma relación que las de las sensaciones.
  • Producción de magnitudes:
    • El sujeto debe ajustar la intensidad de un E con un magnitud dada previamente.

lEmparejamiento de razones
  • Estimación de razones:
    • El sujeto debe indicar la razón o cociente (1/2, 1/3, 1/4...) entre las intensidades de las correspondientes sensaciones.
  • Producción de razones:
    • El sujeto debe ajustar la intensidad de un E variable hasta una relación (1/2, 1/3, 1/4...) prefijada con un E estándar de intensidad fija.

lEmparejamiento de intervalos
  • Clasificación:
    • El sujeto debe clasificar un conjunto de estímulos en categorías de la misma amplitud psicológica
  • Equisección:
    • Dado un intervalo delimitado por dos estímulos, el sujeto debe buscar n E intermedios que lo dividan en subintervalos iguales

lTeoría de detección de señales (TDS)


lOrigen
  • 1950: Crisis Interna dentro de la Psicofísica.
    • Percepción determinada por las características físicas del estímulo y por la capacidad fija del sujeto.
    • La noción de umbral es una hipótesis superflua meramente metafísica (Thurstone, 1927).
  • Experimentos: Mostraron que los sujetos son inconsistentes.
  • TDS
    • Fue propuesta por Tanner y Swets (1953): “Signal Detection Theory and Psychophysics” (1966)
Hipótesis
1ª Hipótesis: "En cualquier actividad humana o en un ensayo siempre hay algún grado de interferencia o de ruido". El ruido procede de varias fuentes internas y externas.
2ª Hipótesis: "No se pueden definir las condiciones para poder medir un umbral perceptivo".
3ª Hipótesis: "El informe del observador de la presencia/ausencia de una señal no sólo depende de la sensibilidad del sujeto sino que también depende de otros factores no preceptivos (criterio de respuesta)".
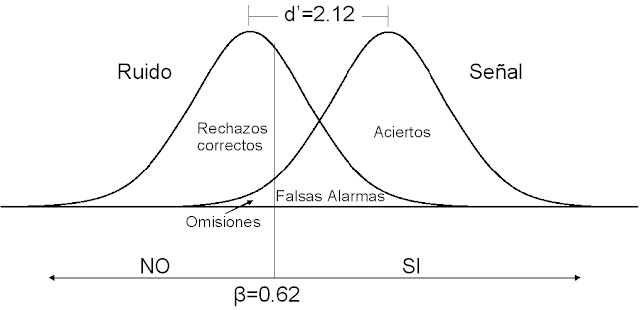
4ª Hipótesis:l "El sujeto/observador debe decidir si lo que experimenta durante el ensayo procede de una distribución de Ruido (R) o de una distribución de Ruido+Señal (R+S)".

Variables
  • Razón Señal/Ruido
  • Probabilidades a priori (prob. de ocurrencia de r y r+s)
    • P (r+s)>P (r)è Criterio Liberal
    • P (r+s)<P (r)è Criterio Conservador
    • P (r+s) = P (r)è Criterio Neutro
  • Matriz de Pagos o Consecuencias
  • Instrucciones (Neutras, Laxas y Estrictas)
 
lProceso Sensorial: Refleja la discriminabilidad del estímulo. 
  • Parámetro: d’ (sensibilidad de respuesta) 
d'=ZP(Si/r) -ZP(Si/r+s)

Proceso Cognitivo: Depende del propio sujeto (motivación, expectativas…)
  • Parámetro: β (criterio de respuesta)

Tipos de respuesta



Curva Característica de Operación del Receptor (COR)
lExpresa la relación entre la probabilidad de A y la probabilidad de FA cuando se mantienen fijas las variaciones del estímulo y el sujeto varía su criterio de decisión.
Permite hacer predicciones de la probabilidad de aciertos, conociendo la probabilidad de falsas alarmas (y viceversa), con indicación del tipo de criterio para cada relación y de la discriminabilidad de los estímulos presentados (o la sensibilidad del sujeto).

Características de la curva
Es continua
Es simétrica respecto a la diagonal
Es creciente
Su pendiente es decreciente

Cálculo de d'

Cálculo de β



Representación Gráfica



Curva ROC



l
l
l
l

l
l
–
l
Suscribirse a: Entradas (Atom)